Receive news, product launches and course info via subscribing to our mailing list here.
Conceptual Subitizing
Topic
Early Number
Grade Level
Year 1, Year 2
Lesson Materials
3 Mental Routines
7 Strategy Lessons
3 Problematized Situations
10 Games
Resources
Compressed Zip File 8 MB
64 printable pages
4 Slide Shows
2 FLASH programs
Select Licence:
About Conceptual Subitizing:
In this book we focus on conceptual subitizing and show how this aspect of subitizing forms the basis for mental computation. In particular the two strategies of counting on, rather than counting all, and doubles develop naturally out of conceptual subitizing. So, what is conceptual subitizing?
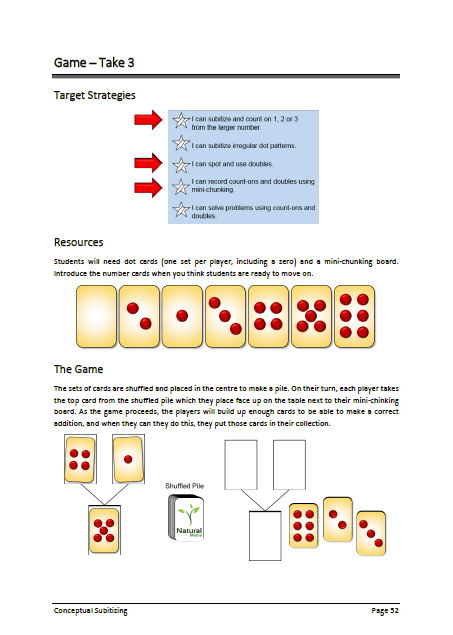
Conceptual subitizing refers to the ability to see groups of objects, to combine the groups mentally and to know how many objects there are in the group. For example, the ability to count on by 1, 2 or 3 from a subitized group is a form of conceptual subitizing.
It is time now, to build a framework for conceptual subitizing, which leads to fluency with early addition facts. Although this may sound trivial, for many students, developing ideas about the concept of altogether requires considerable support. Developmental milestones to watch for include:
- Knowing that written numbers tell how many are in a group and are not the names for the last object counted.
- Knowing that objects can be moved but that the amount in the group remains unchanged.
- Being able to break the counting sequence and count on from a given starting number.
- Combining two groups rather than naming the groups.
When students are first presented with two groups to combine they are likely to count all. If we’re not careful, counting all becomes the default strategy that is used for all later computation. The activities presented here are designed to encourage subitizing and counting on. When students can spontaneously count on they will be ready for the introduction of doubles and rainbow facts. Until that point teaching other strategies is difficult because the basics are not in place.
The Australian Curriculum: Mathematics emphasizes the importance of subitizing and Conceptual Subitizing supports the teaching of Year 1: ACMNA015 and Year 2: ACMNA030.
We have provided a sample from this material to give you a feel for this product. You can download the sample now:
We have also made the changeover from FLASH programs to HTML5 and the next link enables you to check out one of our all-time favourite apps in which you drag the mask down to slowly reveal the cards that it hides and your class try to guess what the cards are before you show them:
Similar ProductsYou may also be interested in...
This bundle includes the Subitizing: Laying the Foundations for Number Sense book and print resources to make regular dot and number cards.
This bundle includes the Visual Scaffolds for Mental Computation book and print resources to make dot and number cards.