Place Value and Measurement
I really enjoyed working with the fabulous teachers at Parafield Gardens Primary School on Monday last week.
During the day we did lots of hands-on mental routines and measurement tasks. One topic, of course, was conversions and the need to have a really deep understanding of place value applied to measurement.
At lunchtime there were three old maths textbooks out on a table with a “Please take me” sign, so I did. You all know by now that I am a bookaholic and avid collector of old maths education books.
Back at home I gave one of the books the flick test just to see if it was of any real interest. For some reason I stopped on this page:

Buried in the 20 questions was Question 17, the one about the water flea. I stopped and seriously struggled to consider:
- “How minute is a waterflea?”
- “What does a waterflea look like?”
- “Would a waterflea be visible to the naked eye?”
Then I scaled it up in my mind by 100 times and was surprised how big it suddenly seemed. In fact, I was quite intrigued and then began to feel quite annoyed that we don’t allow time for curiosity and wonderment in the maths lesson. Nor do we expect students to come to understand how maths can explain and expand our understanding of the world.
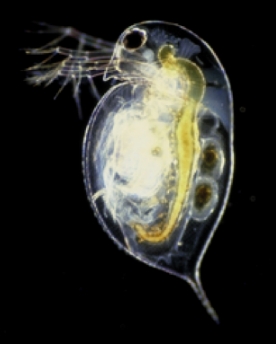
So, what would happen if instead of 20 questions and boring worksheets, we allowed students to actually explore questions such as the waterflea one?
I suspect students would:
- be better at visualizing centimetres, millimetres and microns
- see a purpose in scaling up (or down) in magnitudes of 10
- deepen their understanding of how numbers grow in a base 10 system
- perhaps use a calculator for multiplying by 10
- generalising a rule rather than parroting a rule such as add zero to the end or move the decimal place 2 places to the left. If you haven’t already read 13 Rules that Expire even though we recommended it in our last blog, go and read it now it — is important stuff!
- consider how the scale of a magnifying glass or other tool changes the size of what we are looking at
- actually remember the maths that took place in the lesson. Apparently, after a 15-minute break, most students cannot remember what was on the worksheet they were doing before the break!
There is a strong case for slow maths. So why not get stuck into something that might interest students and get them to connect maths to intriguing actual scenarios?
Problematized Situations is one way to slow and deepen students’ maths experience. Want to learn how?
