Place Value Picture Books

We have just completed a substantial rewrite of our Place Value to a Million and it is now available from our website, here.

One of my favourite parts of finishing off a new product is linking the topic to related picture books. Today I have chosen A Million Dots to share with you.

Although I have had some of the books for a long time, pulling them off the shelves revisiting them and perhaps finding things that I hadn’t really considered before with the new sharper focus is a part that I really enjoy. While picture books for older students do not abound, there are still a variety to choose from.

It took me a moment or two to overcome the fact that the book is full of American references and imperial measurements and to look beyond that to how it could readily be used in an Australian classroom. The teaching learning potential is outstanding and yes, there are actually a million dots in the book.

Every page has something to promote conversation or investigation as well as providing interesting facts based on large numbers. The connections between large numbers and how and where they are used in context and across the strands of mathematics is one of this book’s many assets.

As you flick through the book large numbers are connected to:

Counting
Comparing
Magnitude
Time (seconds, minutes, weeks, years)
Measurement (linear, distance, length, height, circumference, area, volume, mass, capacity)
Ratio (a theme to be explored on every page)

There is a pattern in the increase of dots on every page that students could, with the help of a calculator, identify and use to predict how many dots will be on the next double page spread.

Every page has an interesting large number fact to be explored. The Gray Whale in the page shown below for instance swims 350 000 miles in half of its lifetime.

“How far is that in its whole lifetime?”
“What is that in kilometers?”
“Will it be more or less than 350 000?”
“How many trips around the world or to the moon is that equivalent to?”

I love it when students get into posing and researching their own “I wonder” type questions after being presented with scenarios such as this.

As I looked at the book, I couldn’t help but marvel at the mathematical modelling that must have led to some of the pages and wondering how accurate the numbers actually are. (see Johnny’s note below). Then there was the Soup Can page, presumably inspired by the famous Andy Warhol painting.

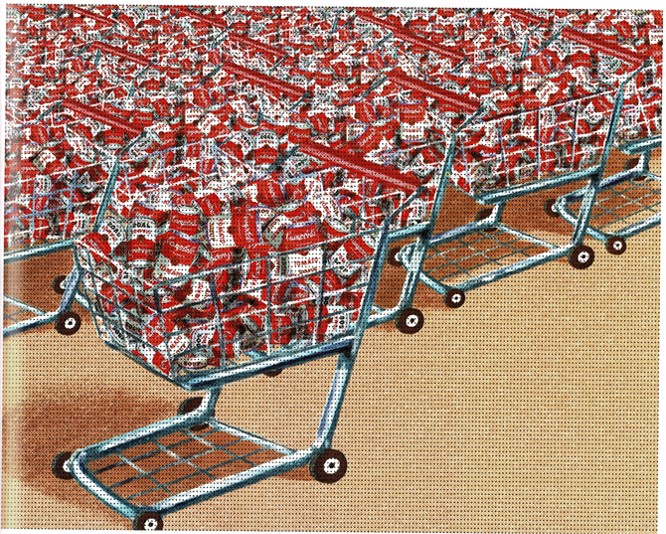
This page really got me thinking:

“Does a grocery cart really hold that many cans of soup? How many cans in a trolley is that anyway?”
“Did the author put cans into carts, or did he use the measurements of the cans and the volume of the trolley? How else could he have done the maths?” I wonder what the students might suggest.
“Is the number of cans actually realistic? How could we check?”
“What if it was cans of baked beans?”

Making conjectures is an important part of maths as is making reasonable estimates. These questions remind me of Fermi problems. I have always loved them. Could be a good lead into finding out about Fermi and what real mathematicians and physicists actually do.

Have a great break; it’s time for one NOW!

Cheers,

Postscript by Johnny

What do we know about 1 million? The first step might be to find its factors. Let’s start with something simpler.

1 000 = 8 × 125
Therefore
1000 000
= 1 000²
= 8² × 125²
= 64 × 125²

A special feature of the book is that the very last page has but a single dot on it, and so there have to be 999 999 dots that precede it. It feels as if the planning stage for the book went along the lines of “Maybe I could find some usable numbers if I subtract 64, rather than 1.” Hence

1000 000 – 64   
= 64 × 125² – 64
= 64 × (125² – 1²)
= 64 × (125 – 1) × (125 + 1)
= 64 × (31 × 4) × (42 × 3)

Now for the important questions:

                “How many pages should there be in the book?”
                “How many dots should there be on each page?”

The answers that the author came up with are 42 pages of pictures and therefore 64 × 31 × 4 × 3 = 23 808 dots on each page. He chose to make rectangles of dots and the best way to make 23 808 dots into a rectangle would be to have 64 × 3 = 192 dots in one direction and 31 × 4 = 124 dots in the other, making a 192 × 124 rectangle of the required 23 808 dots.

Yes, I did check that the rectangles of dots are indeed 192 × 124 and so, thanks, Andrew Clements, you really did treat us to seeing 1000 000 dots in the one book. Thanks a million!