Halloween Blog

Tidying Up

I seem to accumulate so much paper stuff and file it away for later and then end up with stacks that need to be culled. So whenever I have a rare few minutes or hours I go through the stuff. My rule is to handle it once only, to either throw stuff away or use it.

Sometimes I find gems amongst the dross, as is what happened when I stumbled across some student work samples from last Halloween. I have kept them, intending to analyze and share the mathematical developmental information that they show.

So here goes a bit belatedly, but in time for this year’s Halloween.

So let’s begin with the problem:

About the problem

Notice that the numbers used can each be shown as subitizable groups and that a rainbow fact is included, also notice that combining 4 and 2 to make 6 means that a double could be used.

What might we see?

I always think about how different students might handle the problem; I only draw one of each item on the board and write how many next to it. This means that some students begin by simply counting the objects drawn not interpreting the problem as meaning several of each object and usually counting repeatedly because they do not trust the count.

• Some students will count and draw each group but not demonstrate the concept of altogether.
• Some students will draw subitizable groups and then use a count on strategy to find out how many altogether.
• Some students will use fingers and count all or count on.
• Some students will use known number facts.

Examining work samples and annotations can help find out what next for each student.

Work Sample 1

Harrison began by drawing eyeballs without counting and then stopped to count and found he had one too many. He was able to fix it up by crossing the last one off but then went back to the beginning to check. He continued to draw but counted as he went, always going back to the beginning to see how many there were now, counting all each time as you can see from the marks showing that he had touched and counted each time.

Harrison struggles actually writing the numerals and made reversals knowing that he was probably wrong but not using a number line or other tool to help him.

Harrison needs support counting collections, stating how many there are then trusting that there is actually that amount and then counting on. He should also be shown how to find the number he wants to write, trace over it several times and then free write it on his page.

Work Sample 2

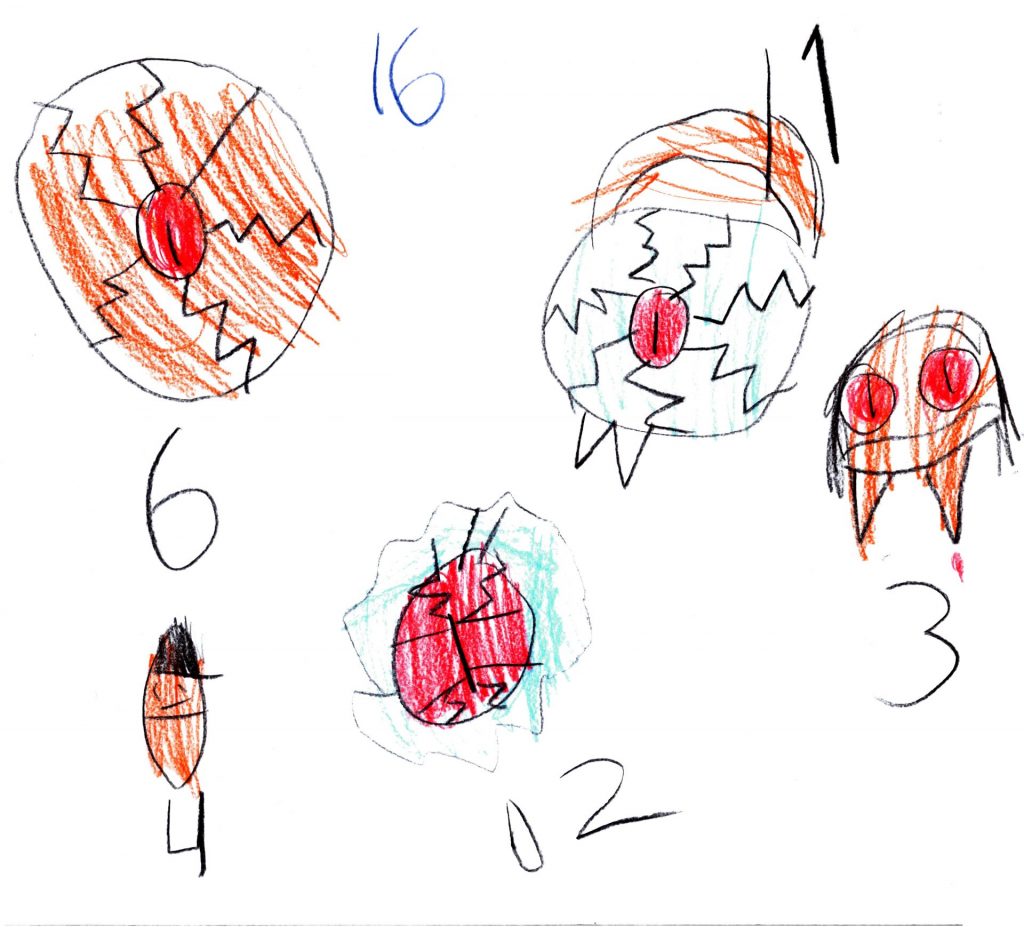
Jacob looked as though he was enjoying an art lesson but when I spoke to him he had already worked out how many altogether by counting all by tapping on each item the appropriate number of times as if he could see them there. This is an important step when students start to compute ‘invisible’ items and will lead to further abstraction.

Prompted, Jacob found the rainbow pair on the rainbow fact poster and said 10 and then counted on.

Jacob should be encouraged to count on from the largest number rather than count all and also to actively spot pairs that he can already add or already knows. The rainbow facts were familiar to him but he had not thought about which strategies might help with the numbers that he had.

Work Sample 3

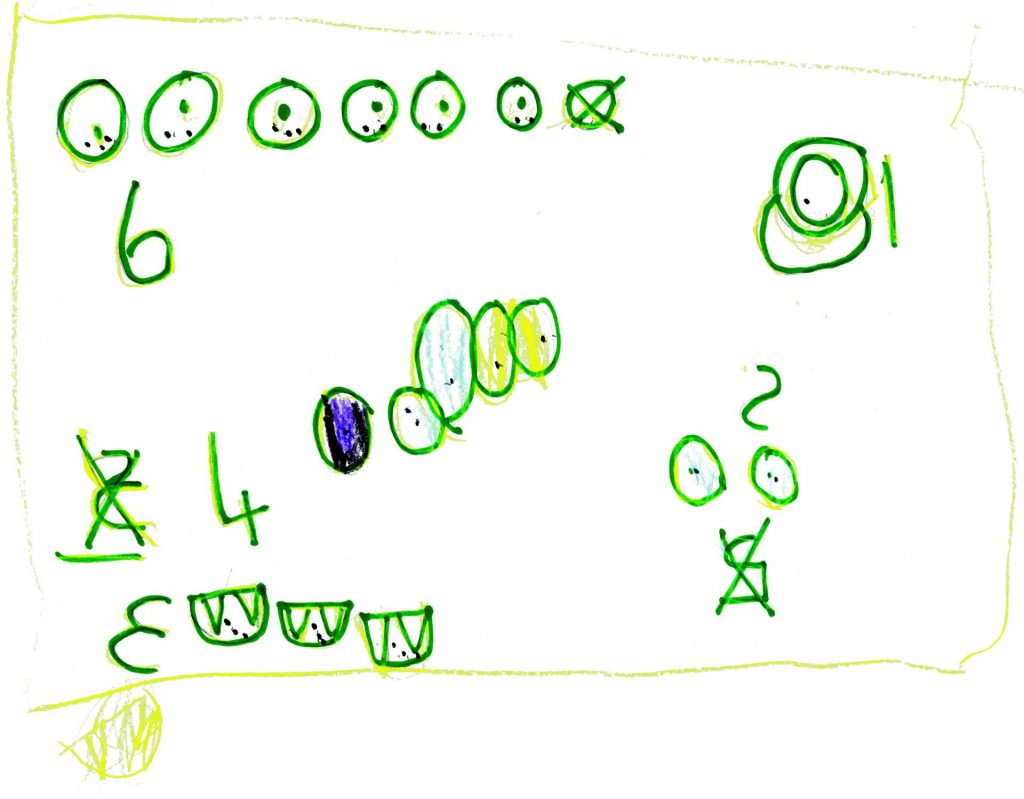
Sevanna was the only student who deliberately used ‘dice’ patterns so that she wouldn’t have to count as she drew. She also deliberately planned to have the rainbow facts together first and then count on all the others. She clearly understands that numbers can be added in any order and that it is a good idea to look for parts that make adding easy.

The question has to be asked as to whether Sevanna actually needs to draw pictures at all. She may be ready to use mini-chunking for addition or an empty number line so that she is moving toward the use of symbols only.

Work Sample 4

Sanjeet started drawing but realized that he really didn’t need to because he could do it in his head. Prompted he explained that he had done 4 and 2 which is 6 then 6 and 3 which is 9 and then 1 which is 10 and then just knew 6 more was 16. Sanjeet is actually working in the abstract; he did not need any visual support.

Sanjeet added the numbers in their given order: we need to check that he knows he can add them in any order and that the answer will not change. He also needs to be prompted to look for efficient and reliable ways of adding mentally that draw on rainbow facts and friendly numbers. He also, like Sevanna, needs to be shown strategies that enable will him to record his thinking on the page.

Learning for us?

Looking at the work samples and listening to students explanations and reasoning, prompting if appropriate are crucial if we really want to find out what our students do know and can do so that we can plan accordingly and differentiate tasks and instruction to ensure that every students is making appropriate growth.

That is the beauty of problematized situations; students can enter at their own level. There are multiple pathways and multiple points that build in success for all and open doors for teachers to plan targeted strategic support and challenge.

For more about problematized situations check out the online course we have created to help you develop your own problems. Have fun!