Number your Easter Eggs
Our Numbered Eggs in the Easter Rings is a series of problems that share the same context and problem. Each level consists of interlocking rings and each space that the rings create holds a number, as in:
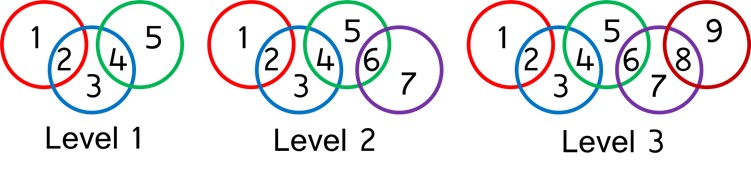
The problem is to position the numbers to make the numbers in each ring add to the same total.
To solve these problems calls for computational thinking as finding a solution almost inevitably involved looking at the patterns within the numbers involved and working on from there. For example, at Level 1, we challenge the students to make the numbers in each ring add to 6. As a teacher, you might prompt a student working on the Level 1 version by asking:
“Can you find three numbers for the middle ring that will have to add to 6?”
If necessary, you might ask another question:
“You didn’t use the 5. Which of those numbers will be in the same ring as 5?”
Similar prompts will work at Levels 2 and 3, where the first challenge is to make the totals all equal to 9 at Level 2 and equal to 11 for Level 3.
In this case, the links to computational thinking are:
- Breaking the [problem down into a series of small, more manageable problems (decomposition). In our case, asking what numbers could be in each ring so that they all have the same total.
- Each of these smaller problems can then be looked at individually, considering how similar problems have been solved previously (pattern recognition). This time looking at the different ways in which a given total can be made and how they might be joined.
- Focusing only on the important details, while ignoring irrelevant information (abstraction). A strategy here would be to cater for the least flexible first, as in finding where the largest number has to go.
- In a definition of computational thinking, the next step is to find simple rules to solve each of the smaller problems (algorithms). In this case, we might even find a way to list all possible permutations of the numbers involved and use a spreadsheet to locate which lead to correct solutions.
If you think your students are ready for a little computational thinking, click here to download our Numbered Easter Eggs in the Easter Rings problems.
I’m sure your student will enjoy them! If you would like to see the solutions that we found, just click here – go on, do it!
P.S. The above steps of computational thinking came from the BBC at this URL:
