Questions can only be as rich as the task
Teachers are beginning to use brain breaks, energizers and number talks to enhance their maths lessons. Students seem to engage well with such techniques. We need to ask though whether these little tasks are rich enough to allow for deep thinking rather than superficial, surface-level thinking.
What do I mean by this? Well in a classroom this week students had come in from break and the following was on the screen ready for the students to think about:
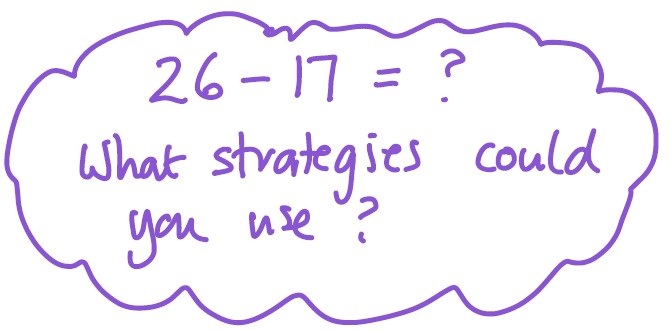
The students sat for a few seconds and then began to share strategies:
- “Count up.”
- “Count back.”
- “Add 1 to 26, take 10, then take the 1 off.”
The teacher recorded the strategies and asked for clarification but that was the end of the discussion. The task was not rich enough to allow for connections to be made and for students to generalise how knowing one thing can be extended and applied to another. Nor did the task allow for differentiation other than in strategy choice.
So we opened up the initial task:
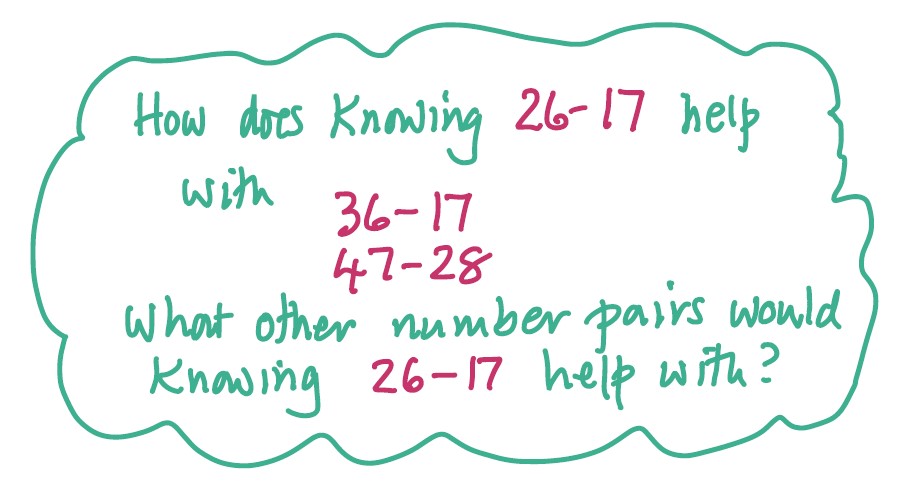
More scope now for questioning and generalising and for stretch.
For example: “What if we had to do these subtractions?”
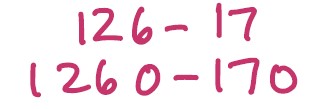
“Does it only work for whole numbers? What if we wanted to know …”
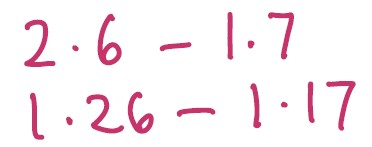
As you may have noticed in the last two blog posts, Place Value and Measurement and Subtraction Gobbledygook
If students say:
“Take out the decimal point, find your answer then put the decimal point back.”
Expect them to explain how and why that works.
They are, in fact, multiplying each number by 10 to create whole numbers and then dividing by 10 to get back to decimals. There is an implicit understanding here of the Distributive Law whereby multiplying by 10 means that each number in the expression 2·6 – 1·7 is multiplied by 10 as in 10 × (2·6 – 1·7) = 10 × 2·6 – 10 × 1·7.
And, if they talk about moving the decimal point, remind them that the decimal point does not move.
The richer questions that can arise from richer tasks will move thinking and learning forward and engage and challenge learners.
One great strategy for creating rich problems are problematized situations – learn how to create them in my online course.
