Today we are exploring polygons.

Polygon is derived from the Greek where poly means many and gon means angle, so a polygon is a many-angled 2D shape made with straight sides because an angle is made by two straight lines, not curved lines. First, we are going to create the simplest type of polygon, one with only three sides – the triangle. Younger students often:

• have difficulty drawing triangles reasonably accurately, they often bend a line or too to make them meet
• do not recognize a triangle if it is not sitting on its base like this:

They will say these are not triangles:

They do not look closely enough or attend to the properties carefully. As a result, they may incorrectly identify both of the following as triangles:

One older student asked me whether the triangle was the space inside the lines or outside the lines.

Let’s get started

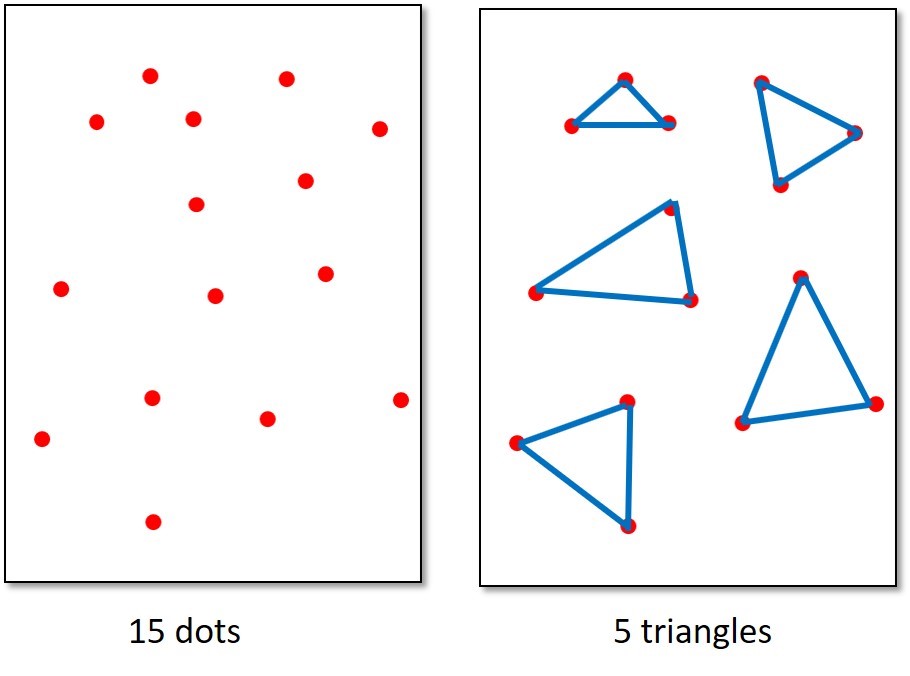
The first task is to draw 15 well-spaced dots on an A4 piece of paper and then using a ruler to carefully draw sets of 3 dots to create 5 triangles. Students should describe and older students name them.

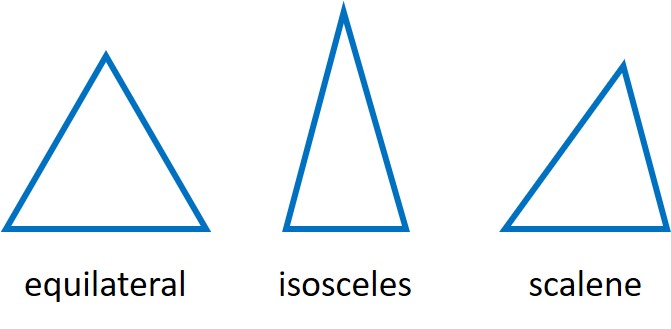
Triangles can be sorted by the features of their sides:

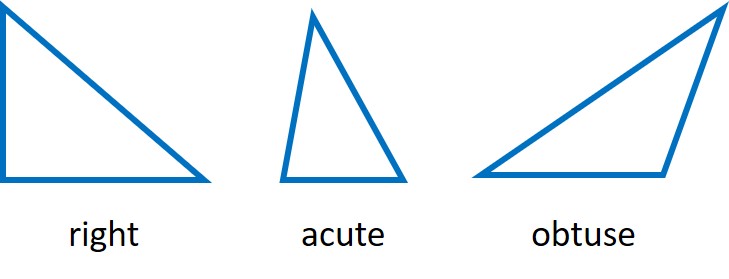
or by the size of their angles:

The second task is to draw a line from one angle (corner or vertex) of a triangle to the opposite side and colour one of the new triangles. Now draw a line from the unused vertex to the new line and colour the two new triangles.

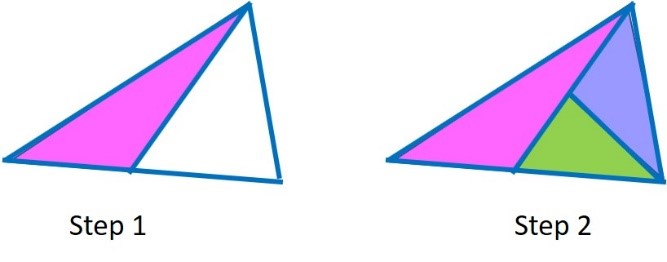
Older students can pose some What if’s, such as:

• “Can I make 1 or more than 1 right triangle inside each big triangle?”
• “Can I make one of each type of side or angle triangles in each big triangle?”

I looked at my triangles and wanted to put a sky with clouds behind them and turn them into kites. When the maths is done, turn it into fun.

Quadrilaterals

Most people think of squares, rectangles, parallelograms, trapezoids when they think of quadrilaterals and many students are unfamiliar with the term irregular shape. In fact, more than one has said that irregular shapes are not actually shapes. So, lots of reasons to explore quadrilaterals.

For this activity draw 20 well-spaced dots on the page and join sets of 4 dots to make 5 quadrilaterals. You might need to cheat a bit, I had one that joined up to look like a triangle so needed to adjust the dot!

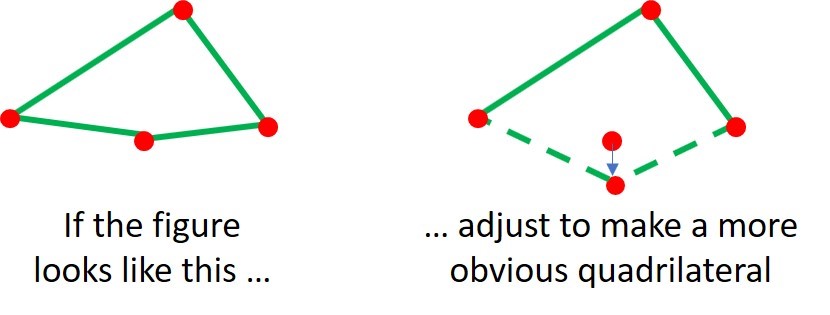
Students should be able to explain and predict whether a quadrilateral will create right angled triangles and should notice the opposite angles are equal to each other. Some students can use their protractors to measure the angles.

Have fun, like I did!

I thought my coloured triangles made the quadrilaterals pop up and look like pyramids, so I felt a desert scene or pirate map background coming on.

Cheers … and enjoy your Technicolour Tuesday!