The Lion’s Share
Book 2 in our Multiplicative Thinking Series focusses on doubling, repeated doubling, halving and repeated halving, all of which are important strategies for moving toward flexible multiplication and division strategies. With this in mind, I have chosen “The Lion’s Share’ as the second book in this series.
The Lion’s Share makes visible the exponential changes in magnitude when repeatedly doubling or halving a number.
Connections between Division, Halving and Fractions
Fractions are often introduced in a separate unit to division as though they have nothing to do with division. When we are dividing, we are actually sharing into equal parts, or finding a fraction of something.
Students may get all the way through school without ever making these multiplicative connections between the two. The first part of the Lion’s share connects division and fractions really well, making it visible that the more cuts into the birthday cake, the smaller the parts become but the larger the number of parts become. The vocabulary, half, middle, quarter, remaining, half of what’s left provide a rich starting point for repeated halving and naming resulting fractions. The inside back cover shows the fractions proportionally all the way to 1/128.
This provides opportunities to talk about how the size of the denominator relates to naming fractions and to the size of the parts and the number of parts the whole has been divided into. Students need to be challenged to explain the process and the role of the denominator in a fraction.
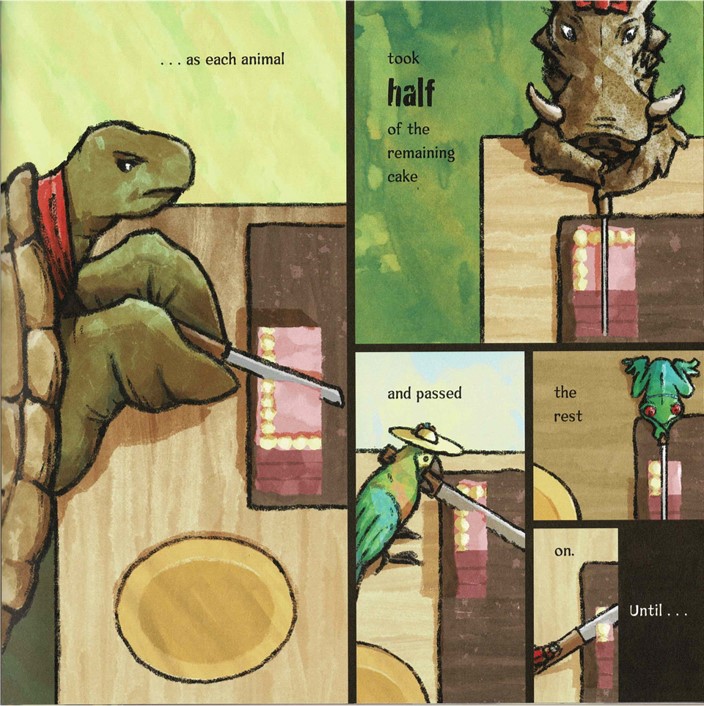
Inverse Operations: Connections between Repeated Halving and Repeated Doubling.
The second part of The Lion’s Share is about doubling, and we soon see that doubling has the opposite effect of halving, with each double the quantity increases. The numbers grow very rapidly when doubling and students may notice that the whole numbers match the denominators presented in the first part of the book.
Arrays are chosen as a visual strategy to show the exponential growth patterns to 256.
Arrays are an important tool in multiplication and lead to an understanding of the commutative property of multiplication, 2 × 8 gives the same product as 8 × 2.
To show the distributive property of multiplication, an array can be broken into smaller parts for flexible multiplication strategies for unknown facts.
Understanding the Area Model for Multiplication.

What if questions could be asked about the arrays. For instance, looking at the 128 array pictured above, we can ask,
“What if you wanted to prove that there are actually 128 in the array?”
“How could you do it without having to count them all?”
“if you did not just know __ × __, how could the array be partitioned or looped to make that multiplication more manageable?”
The mantra always is
“What do you know that can help you with this?”
Here is one example showing how the array can be looped to match the following known facts:
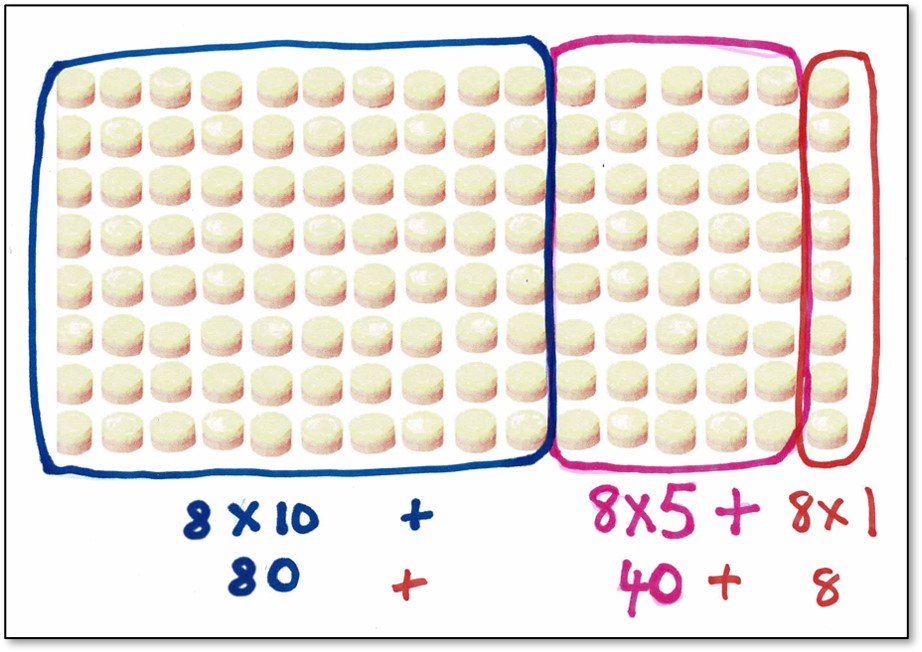
I know that 8 × 10 = 8- so I can loop 8 × 10. I know that 8 × 5 is half of 8 × 10. so I can loop that bit and then I have 8 × 1 left at the end.
Once the visual has been used and understood, it is a small step to working more abstractly with the distributive property for multiplication.
For more about multiplication, check out these Natural Maths Titles:
Building Multiplicative Strategies
Have a great week

