Who Really is the Best at Maths in Your class?

What are we judging maths ability by? Have you thought about problematized situations as a form of assessment? I ask, because some of the strengths of the Natural Maths problematized situations are that they:

• are easy to contextualize, making them relevant to what is currently topical and of interest to students,
• offer opportunities for in depth diagnostic formative assessment to happen,
• have multiple entry and exit points and as such have built in differentiation,
• identify what follow up activities and core learning need to follow from the identified strengths and weaknesses.

An Easter Egg Problem

As Easter is just around the corner, in a demonstration lesson last week I presented the above problematized situation. The teacher whose class I was in was genuinely surprised and perhaps perturbed by some of the responses.

From the Top Mathematician

Her top mathematician, let’s call him Z, sat on the carpet and called out “The answer is 7” almost as soon as the problem was delivered. I could see most students accept that as he was always right then 7 was the answer. Some students thought they had nothing else to do until I said that I was not sure about his answer and that when he put his thinking on the page I would come and see how he got his answer. Z didn’t look too happy but went to his desk like everybody else. The teacher looked at me and said she thought the problem was too hard because of all the words and that he was best in the class with his automaticity in number facts and tables and always wanted bigger numbers. However, she could soon see that most students knew they had to work out 8 lots of 8 as the first part of the problem.

I went to Z quite quickly to find out what he was thinking. At this stage there was nothing on his paper. When asked what he had done to get the answer, he told me it was a take-away. Asked why he said because the question said how many left which is always a take-away. Key word strategies often backfire when a word such as left is used differently to what is the expected norm. [Maths language is a funny beast.] Asked to record what he had just told me, Z wrote:

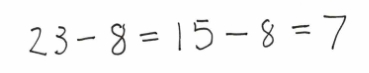
And then looked at me as if I were not too smart. When I asked him what 8 packets with 8 eggs in each packet would be, he looked at the problem again and frowned. I offered him time to think and said I would come back when he was ready. When I did get back, he had written 8 × 8 = 64 and said he just knew that. He was still struggling though to decide what to do next. When asked what Mrs Green wanted to do, he smiled and said, “Oh share the eggs.” I left him again, quite sure that he would have a procedure for that.

From a Mid-range Student

Meanwhile I moved on to what the teacher described as a mid-range hard-working student, let’s call him Y, who had written the following:

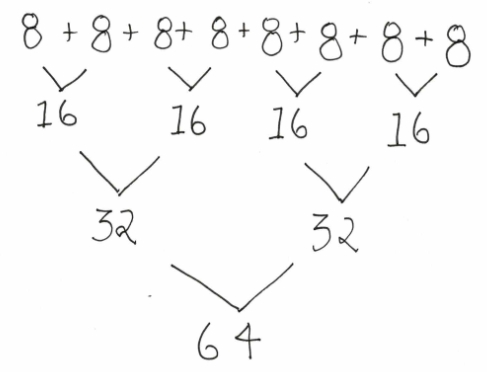
When asked what he needed to do next he said, “Take away 23 and keep taking away 23 until I can’t take 23 anymore and then I will know what is left.” He looked up and said “23 + 23 is 46 so I will start with that.” and wrote:

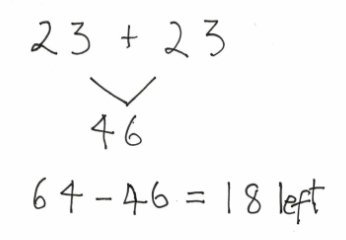
From a Struggling Student

Now let’s look at a struggling student, let’s call him X, who began very slowly drawing a box with 8 eggs, some detail on the first two eggs and then 6 more eggs, subsequently followed by dots in the boxes as he counted on in 2s each time. We can see how he accommodates changes based on lack of space and knowledge of friendly numbers. The answer 64 eggs is arrived at by skip counting in 2s until 40, when 40 and 8 more was a known friendly number fact. Okay, so X did not finish the second part of the problem but knew he had to share the eggs and planned on drawing 23 circles for students and sharing the eggs till he could see what was left. Not an efficient strategy but it will work.

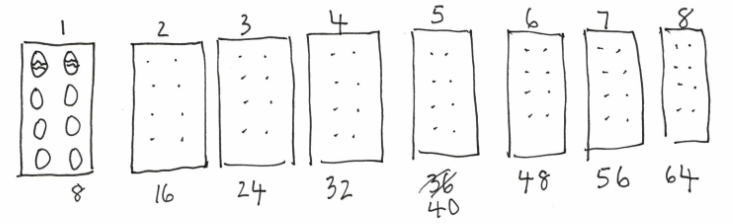
It seems to me that the two students, X and Y, were able to unpack that this was a multiplication and sharing problem even though their strategies were not yet fully multiplicative. Student Y knew that he had to count in 8s eight times and used a repeated doubling strategy to get there: this is almost multiplication. Student X also knew via a visualization of arrays that this was a multiplication problem which he solved additively by skip counting. Let’s come back to student Z who after a challenge and a prompt recognized the multiplication needed and knew 8 × 8 by rote. I cannot help asking,

What mathematical power did each student demonstrate?

Who actually is the best at maths? Was it:

1. The procedural thinker who needed prompts to get started and to understand the problem?
2. The student who could show using numbers and repeated doubling how many eggs?
3. The student who drew a diagram to make sense of the problem and began to invent shortcuts?

The beauty of problematized situations is that they show exactly what mathematical power a student brings to the problem, and, yes, there is always some mathematical power to be found and pointers as to what timely teaching and stretch is needed next.

To learn more about problematized situations, take a look at our online Problematized Situations Course. This week I’ll be posting a few Easter-themed problems. I hope you are able to enjoy them with your class!

Best wishes for a Happy Easter!