Help or Hindrance?

Teachers often tell me that they find it hard to cater for the diverse learners in their classes and that they don’t get around to their more capable mathematicians because it takes ages to explain, show and scaffold for their lower entry point students who need lots of help to get started, take a risk or get motivated.

To my mind, we need to think about what we are actually doing when we move in too soon to help a struggling learner.

I just googled ‘maths help’ images and selected these two cartoons to make a few points. But before I do, peruse each image and look for positives and negatives that might arise from the form of interaction presented (okay this is only hypothetical and we have no real insight into the intent but it might stimulate good discussion).

I looked at Image 1 and it seemed as though each person is smiling. But then I looked again and saw:

• the teacher standing over the child not at child’s level
• the teacher’s mouth open; is she doing all the talking and telling?
• no eye contact; surely we need to watch student’s reactions and feelings so that we can check for comfort and usefulness or acceptance of feedback,
• no other students nearby to benefit from the instruction.

To me it is images of this nature that perpetuate the idea that the teacher is the ‘font of all knowledge’, who teaches what it is she wants the student to learn rather than find out what they are ready for so that she can facilitate the learning students next need.

Research tells us that when you ask a student “Do you understand?” they might say “No” once, but after a second explanation and again asked “Do you understand?” will say “Yes” because by now they are feeling really stupid.

Okay harsh? But I want to foreground thinking and talking about what a useful interaction could look like, particularly with our less confident learners.

So Image 2? At least the teacher is sitting at eye level and it looks as though the two students sitting opposite each other might be checking understanding with each other.

Is the girl on the end pointing to something of interest to contribute?

Still we need to ask “Who is doing the thinking and the talking?” After all it is her mouth that is open. And what about the boy with his back to us and arms folded. Is he rolling his eyes or anticipating that any minute now she will just tell him the answer?

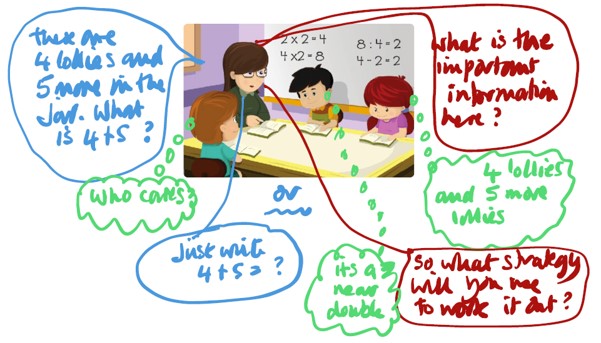
So back to the issue, how can we differentiate and provide for the whole class but, in particular, for those who have disengaged or who struggle?

Some strategies for differentiation are to:

• ask questions that allow students to do the thinking rather than to dumb it down, so that no thinking is required
• observe, listen and notice what students do know and can do and then modify the task so that all students have an entry point
• use mixed ability groupings wherever possible and encourage, in fact teach, quality maths interactions
• sit at one table and interview a student, coaching a little and you will notice the other students listening and sometimes rethinking their approach or suddenly able to get started without your direct instruction,
• give constructive feedback rather than telling, e.g., “Yesterday you drew a diagram to sort out the problem and that was very powerful for you. Would that work today?”
• put up a poster that says the brain only sparks if you make mistakes and struggle with an idea, no pain no gain
• reflect on mistakes, fix-up strategies and multiple representations so that all students can buy in.

No doubt you will have some powerful ideas to add to this list. Have a great term!

Want to know more about my approaches? Check out my Natural Maths website here.