Flexible Conceptual Subitizing
“We did subitizing for the first three weeks of term and now we’ve moved on.” I was told recently as I proposed we do a problematized situation based on subitizing. I did the lesson I had planned anyway because I knew from past experience that we sign off too soon on subitizing. The teacher was quite surprised by what she did and didn’t see and soon realized that students need to subitize every day and they need to do more than simply identify and name subitizable groups. Most students counted all as they represented their groups of ten and some recounted because they did not trust the count. A few started with a subitizable group and as far as we could tell only two students organised themselves with at least two subitizable groups to represent either a double or a rainbow fact.
A quick refresher
Subitize means to immediately know without counting how many there are. There are common recognisable patterns such as the ones found on dice and dominoes.

These are perceptual subitizing patterns and are discussed in our publication Subitizing: Laying the Foundations for Number Sense.
Conceptual subitizing happens when an irregular pattern or combination is presented which needs the brain to focus on the whole and its parts

The brain will most probably see 4 and 1 more and the result 5 is quickly arrived at – this form of subitizing is the focus of our publication Conceptual Subitizing.
Flexible conceptual subitizing is the stage when students are able to describe the same subitizable pattern in many different ways. Prior to this stage students would identify only one way of describing a pattern and be unable to see that it could simultaneously also be a different combination.
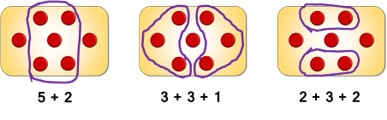
The Problematised Situation – Making Groups of 10
Last night Kai was sorting his counters into groups of 10. He invented a rule for his sorting. The rule was that you should be able to look at each group and just know there were 10 each time without having to count them one by one.
He found a few different ways. I think you are so mathematical that you will find quite a lot of ways of doing this. Here is one of his ways:

Note: Involve students in flexibly describing what they are seeing and thinking before letting them loose with the problem. You will want some of your students to be creating matched mathematical number sentence or equations.
This is an open-ended task in so far as there are many possibilities for making 10 each time. As the students work pay particular attention to:
- who counts all,
- who creates a subitizable group and counts on,
- how flexible they are with conceptual subitizing,
- who plans and uses 2 or more subitizable groups,
- which addition strategies they choose to use, co – count on, d – double, rf – rainbow fact, nd – near double.
Coincidentally, it was wonderful to get this message from Woodcroft Primary:
My Year 4/5 class at Woodcroft Primary School have been revising The Secret Code these last few weeks. Yesterday the big screen dice brought up 9 + 7 and the kids had to name the best strategy to use. A couple of kids shared the birth of a new one that we love and have named SD – Split and Double. Our definition is that when two numbers are an even number apart from each other, split the gap between them and double. For example: 7 + 5 is the same as 6 + 6. We realised we could use this strategy only when the numbers are 2 or 4 or 6 apart and not (easily) when an odd number apart. After 6 it started to become complicated and it was easier to use a different strategy. We wondered if anyone else has ever named this strategy?
So here is a new strategy that you might see in action, sd – split and double and that could even be extended to snd – split and near double – to use when you have an odd number apart!
There are games, problems and mental routines in Visual Scaffolds for Mental Computation to help with this. Let us know how you get on.
Have a great week. I am in Mt Gambier this week working on an exciting project which I will share soon.
Cheers,

